Pulsar Search


Next: Discussion
Up: Analysis
Previous: Radio versus X-ray
A pulsar search of the x-ray data was carried out for two epochs,
one when the x-ray flux was high and one when the flux
was low. Two methods were used to search for periodic
variations. As a quick initial check we used the FFT algorithm provided in the
standard PROS x-ray analysis software.
Data gaps were replaced by the average count rate.
In 1987, E.T. Jaynes (1987)
derived the Fourier transform statistic directly from the principles of
Bayesian probability theory. In the process he demonstrated that it
was optimum for the detection of a single sinusoidal signal in the
presence of Gaussian white noise. A corollary is that for any other
problem (i.e. non sinusoidal lightcurve, and or non Gaussian white
noise) use of the FFT is not optimal.
As a second search technique, we employed the Gregory-Loredo Algorithm
(Gregory and Loredo 1992, 1993): a Baysian method for detecting a periodic
signal of unknown shape in a Poisson time series. This method uses Bayes's
theorem to address both
the signal detection problem and the estimation problem of measuring
the characteristics of a detected signal.
To address the detection problem Bayes's theorem is used to compare a
constant rate model for the signal to a class of models capable of
accounting for a periodic structure of arbitrary shape. The periodic models
describe the signal plus background rate as a histogram in 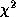 bins per
period, for various values of
bins per
period, for various values of 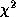 . The Bayesian posterior
probability for a periodic model contains a term which quantifies
Ockham's razor, penalizing successively more complicated periodic models
for their greater complexity even though they are assigned equal prior
probabilities. The calculation balances model simplicity with goodness
of fit, allowing us to determine both whether there is evidence for a
periodic signal, and the optimum number of bins for describing the
structure in the data.
The method readily handles data gaps and the outcome
does not depend on the number of periods examined, but only on the
range examined. The probability of the class of periodic models as a
whole is found by marginalizing (integrating) over all the shapes it can
describe. A special feature of this choice of periodic models is that the
needed marginalizations can be performed analytically, leading to an
algorithm with computational speed comparable to that of the popular
epoch folding method based on
. The Bayesian posterior
probability for a periodic model contains a term which quantifies
Ockham's razor, penalizing successively more complicated periodic models
for their greater complexity even though they are assigned equal prior
probabilities. The calculation balances model simplicity with goodness
of fit, allowing us to determine both whether there is evidence for a
periodic signal, and the optimum number of bins for describing the
structure in the data.
The method readily handles data gaps and the outcome
does not depend on the number of periods examined, but only on the
range examined. The probability of the class of periodic models as a
whole is found by marginalizing (integrating) over all the shapes it can
describe. A special feature of this choice of periodic models is that the
needed marginalizations can be performed analytically, leading to an
algorithm with computational speed comparable to that of the popular
epoch folding method based on  . The odds is defined as
the ratio of the posterior probability of the periodic class as a whole
to the probability of the constant model. A detection is indicated by an
odds greater than one. Once a signal is detected the method employs
Bayes's theorem to rigorously estimate the various parameters of the
signal, such as the frequency and shape of the lightcurve. For a
detailed comparison of the Gregory-Loredo and epoch folding methods
see Gregory and Loredo (1995).
. The odds is defined as
the ratio of the posterior probability of the periodic class as a whole
to the probability of the constant model. A detection is indicated by an
odds greater than one. Once a signal is detected the method employs
Bayes's theorem to rigorously estimate the various parameters of the
signal, such as the frequency and shape of the lightcurve. For a
detailed comparison of the Gregory-Loredo and epoch folding methods
see Gregory and Loredo (1995).
Neither the FFT nor Gregory-Loredo methods yielded a significant periodic signal
detection in the range 1.5 milliseconds to 3000 s.
Our conclusions for periods below about 10
milliseconds are probably unreliable as the accuracy of the final
corrected photon arrival times is probably of the order of 1 millisecond.


Next: Discussion
Up: Analysis
Previous: Radio versus X-ray
Glen Young
Wed Apr 26 17:21:11 MDT 1995
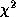 bins per
period, for various values of
bins per
period, for various values of 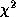 . The Bayesian posterior
probability for a periodic model contains a term which quantifies
Ockham's razor, penalizing successively more complicated periodic models
for their greater complexity even though they are assigned equal prior
probabilities. The calculation balances model simplicity with goodness
of fit, allowing us to determine both whether there is evidence for a
periodic signal, and the optimum number of bins for describing the
structure in the data.
The method readily handles data gaps and the outcome
does not depend on the number of periods examined, but only on the
range examined. The probability of the class of periodic models as a
whole is found by marginalizing (integrating) over all the shapes it can
describe. A special feature of this choice of periodic models is that the
needed marginalizations can be performed analytically, leading to an
algorithm with computational speed comparable to that of the popular
epoch folding method based on
. The Bayesian posterior
probability for a periodic model contains a term which quantifies
Ockham's razor, penalizing successively more complicated periodic models
for their greater complexity even though they are assigned equal prior
probabilities. The calculation balances model simplicity with goodness
of fit, allowing us to determine both whether there is evidence for a
periodic signal, and the optimum number of bins for describing the
structure in the data.
The method readily handles data gaps and the outcome
does not depend on the number of periods examined, but only on the
range examined. The probability of the class of periodic models as a
whole is found by marginalizing (integrating) over all the shapes it can
describe. A special feature of this choice of periodic models is that the
needed marginalizations can be performed analytically, leading to an
algorithm with computational speed comparable to that of the popular
epoch folding method based on 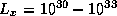 . The odds is defined as
the ratio of the posterior probability of the periodic class as a whole
to the probability of the constant model. A detection is indicated by an
odds greater than one. Once a signal is detected the method employs
Bayes's theorem to rigorously estimate the various parameters of the
signal, such as the frequency and shape of the lightcurve. For a
detailed comparison of the Gregory-Loredo and epoch folding methods
see Gregory and Loredo (1995).
. The odds is defined as
the ratio of the posterior probability of the periodic class as a whole
to the probability of the constant model. A detection is indicated by an
odds greater than one. Once a signal is detected the method employs
Bayes's theorem to rigorously estimate the various parameters of the
signal, such as the frequency and shape of the lightcurve. For a
detailed comparison of the Gregory-Loredo and epoch folding methods
see Gregory and Loredo (1995).