Il biliardo - La teoria dei centri multipli

http://www.millecose.it/biliardo/centri.htm (Internet on a CD, 07/1998)

La teoria dei centri multipli, oltre ad indicare validi ed esatti punti di riferimento, consente al giocatore avveduto di memorizzare i limiti d'esecuzione avvalendosi della posizione della bilia battente ed usando il sistema della proiezione della stecca dalla parte dell'impugnatura.

Definiamo M.N.O.P. campo di gioco reale (il rettangolo verde qui di fianco), indichiamo con O il suo centro ed immaginiamo, immediatamente sotto ed alla sua destra, un'altra area uguale il cui centro indichiamo con 1. Sull'area con centro O stabiliamo a caso un punto B e traguardiamo il centro 1: poiché questo centro è simmetrico al centro O rispetto al lato OP, la traiettoria si riflette (nel punto Q) e si indirizza verso il predetto centro O.
Altrettanto avviene con la bilia posta nel punto B' traguardata col centro 1 in basso: questo centro è simmetrico al centro O rispetto al lato MP.
Nella parte inferiore destra si nota un'altra area il cui centro è stato indicato con 2: traguardando la bilia posta in B'' con questo centro, la traiettoria porterà verso il centro O dopo essersi riflessa due volte in Q'': infatti il centro 2 è simmetrico al centro 1 (rispetto alla proiezione di MP) che è a sua volta simmetrico rispetto ad O, come detto prima.

Ed ecco la tavola generale, con alcuni esempi gia tracciati: lasciamo a voi di provare a trovarne di nuovi e di sperimentarli in pratica.
La teoria dei centri multipli venne per la prima volta dimostrata in pubblico grazie alla precisione di un biliardo fornito dalla ditta Hermelin di Milano e montato per l'occasione; apposite palline segnaletiche vennero opportunamente ubicate intorno a rappresentare i centri delle aree circostanti, come indicato nella tavola qui sotto.

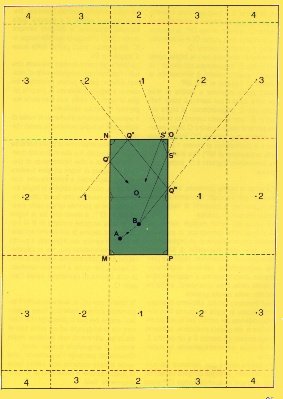Nell'esempio fornito, abbiamo di proposito situato la bilia nel punto B in corrispondenza del centro del quadrato inferiore, da questa posizione, abbiamo traguardato un centro 3 ed un centro 2, riflettendo simmetricamente le traiettorie.
Possiamo notare che, partendo dal punto prescelto, la bilia dirigerà verso i birilli urtando la sponda lunga OP poco dopo la mezzeria in Q''' mentre traguardando il centro 2 e sempre dalla stessa posizione, si dirigerà sempre verso i birilli urtando la sponda lunga in S''.
La teoria dei centri multipli prevede che tutti i tracciati non tengano conto di nessun effetto: per le prove pratiche i tiri vanno eseguiti colpendo la propria bilia al centro o nella sua mezzeria superiore in senso verticale.

Il sistema funziona anche se si tratta di indirizzare la bilia avversaria verso i birilli.
Supponiamo infatti che la bilia battente si trova nel punto A e che in B ci sia quella avversaria e che circostanze di gioco ci impongano di tirare un "Giro". E' evidente che, con la propria, occorrerà colpire la bilia avversaria in maniera che quest'ultima vada ad urtare la sponda lunga nello stesso punto Q'''. E' altresì ovvio che, se la bilia avversaria, anziché trovarsi in B si trovasse una decina di centimetri spostata verso il centro del biliardo, il punto Q''' non servirebbe più, ma si calcolerebbe automaticamente il punto X che, di natura, verrebbe a trovarsi spostato di una decina di centimetri verso l'angolo O.